73. 다음은 두 문서의 용어 벡터(term vector)이다. 이 두 벡터 간 코사인 유사도(cosine similarity)의 계산 결과로 올바른 것은?
 |
▣ 코사인 유사도(Cosine Similarity)
- 코사인 유사도는 벡터간의 코사인 각도를 이용하여 서로간에 얼마나 유사한지를 산정
- 각도를 유사도로 판별하기 때문에 거리가 중요하지 않을 경우 사용되는 방식
- 코사인 유사도는 -1 ~ 1 사이의 값을 가지며, 벡터들의 방향이 완전히 다를 경우 즉 각도가 180도 일 경우에는 -1이고, 방향이 완전히 동일하면 1이며, 값이 90도의 각일 경우 0 값을 가짐
- 적용 : 다차원의 양수 공간에서의 유사도 측정(정보검색, 텍스트마이닝), 두 문서의 유사도 측정
* 계산공식
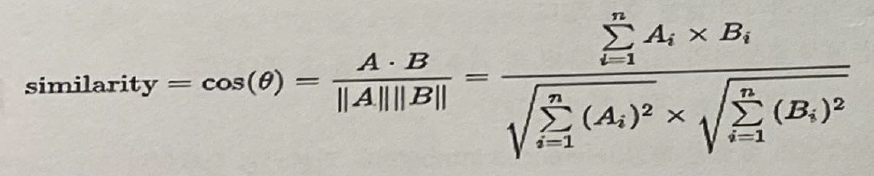
<문제풀이>
- 벡터 표현 Doc1 = [3,1,0,3,1,2,1,0], Doc2 = [1,1,2,1,0,2,4,3]
1) 분모계산 : 두 벡터 크기의 곱 계산하면
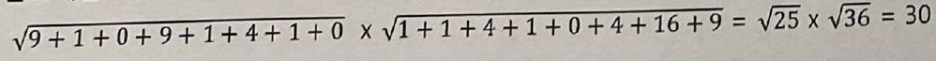
2) 분자계산 : 벡터의 내적
(3*1) + (1*1) + (0*2) + (3*1) + (1*0) + (2*2) +(1*4) + (0*3) = 15
3) 최종 = 15/30 = 1/2 = 0.5
정답 : ②
74. 릴레이션 R을 릴레이션 R1과 R2로 분해할 때 바람직한 분해(decomposition)에 대한 설명으로 가장 적절하지 않은 것은? (단, R1∩R2는 R1과 R2의 공통 속성을 의미한다.)
① 손실없는 분해(lossless decomposition)가 되어야 한다.
② 함수적 종속성(functional dependency) R1∩R2 →R1 과 R1∩R2 → R2 를 모두 만족하여야 한다.
③ R1∩R2 가 R1 의 수퍼키가 된다.
④ R의 함수 종속성은 분해 후에도 가급적 보존되어야 한다.
▣ 릴레이션 R의 R1,R2 분해 → (원칙) 무 손실 분해가 되어야 함
① 손실없는 분해(lossless decomposition)가 되어야 한다.(O)
② 함수적 종속성(functional dependency) R1∩R2 →R1 과 R1∩R2 → R2 를 모두 만족하여야 한다.
예) 이행함수 종속성 존재 릴레이션의 분해(3정규화)
R(A,B,C), 주키 : A, 함수적종속성 : A → B, B → C
* 정규화에 따른 무손실 분해 수행 R1(A → B) / 주키는 A, R2(B →C) / 주키는 B
* R1 ∩ R2 속성은 B이므로 B가 모든 R2의 모든 속성을 결정하나, R1의 모든 속성을 결정하지 못함.
그러므로, 모두 만족해야 하는 것은 잘못된 설명
③ R1∩R2 가 R1 의 수퍼키가 된다.
* 위의 예제에 따라 분해된 릴레이션 중의 하나에 수퍼키가 될 수 있다(유일성 만족)
④ R의 함수 종속성은 분해 후에도 가급적 보존되어야 한다.
* 위의 예제에 따라 R 릴레이션의 함수 종속성이, R1, R2 릴레이션에 보존되어 있다.
정답 : ②
75. 연관 규칙 생성을 위한 Apriori 알고리즘을 사용하여 {A,B,C,D}(간략히 ABCD라고 함)가 빈발 항목집합(frequent itemset)임을 알았다. 그런데, ABCD에서 만든 규칙 BCD→A가 최소신뢰도 조건을 만족하지 않아 연관규칙이 될 수 없다면, 이 사실로부터 더 이상 고려할 필요가 없는 규칙들로만 짝지어진 것은?
① BD→AC, AB→CD
② AB→CD, A→BCD
③ BD→AC, D→ABC
④ A→BCD, D→ABC
▣ Apriori 알고리즘 - 지지도(Support) 를 이용해 연관규칙을 찾는 기법
- A가 B의 부분집합이라면, A의 Support 는 B의 Support 보다 크거나 같음
If A ⊆ B, then support (A) ≥ Support(B)
- 그러므로 B의 Support 가 우리가 설정해 놓은 minimum Support 값보다 크다면, A의 Support 또한 minimun Support 보다 크게 됨
If A ⊆ B and support (B) ≥ min_sup then then support (A) ≥ min_sup
<풀이>
ABCD 는 빈발항목 집합 → 만든 연관 규칙인 BCD → A가 최소신뢰도 조건을 만족하지 않아 연관 규칙이 될 수 없다면, 더 이상 고려가 필요 없는 규칙
BCD → A 연관규칙의 신뢰도 구하면 Pr(A∩B∩C∩D)/Pr(B∩C∩D) 가 된다
그리고 해당 값은 최소신뢰도 조건을 통과하지 못하였으므로 분모가 커지는
Pr(B∩C∩D) 의 지지도(Support)가 커지는 것들을 대상에서 제외 해야 함
* 위의 Apriori 알고리즘에 따라서 BCD의 부분 집합인 B, C, D, BC, BD, CD 는 BCD 보다 지지도(Support) 가 크거나 같아지고, 전체 신뢰도 값은 더 낮거나 같아지므로, 고려 대상에서 제외함
정답 : ③
공감과 댓글은 아이티신비에게 큰 힘이 됩니다.
블로그 글이 유용하다면 블로그를 구독해주세요.♥
'정보시스템 감리 기출해설 > 데이터베이스 해설' 카테고리의 다른 글
| (제 22회) 데이터베이스 / (71)~(72) 해설 (0) | 2024.12.03 |
|---|---|
| (제 22회) 데이터베이스 / (69)~(70) 해설 (0) | 2024.12.02 |
| (제 22회) 데이터베이스 / (67)~(68) 해설 (1) | 2024.12.01 |
| (제 22회) 데이터베이스 / (65)~(66) 해설 (0) | 2024.11.30 |
| (제 22회) 데이터베이스 / (63)~(64) 해설 (2) | 2024.11.29 |