최단경로 알고리즘

문제6) 다음에 대하여 설명하시오.

가. 최단경로 알고리즘의 유형 4가지

나. 다음 그래프에서 4가지 알고리즘 계산 방법

A, B, C, D, E 5개 노드로 구성된 그래프(A가 출발지, E가 목적지임)

다. "나"의 4가지 알고리즘 계산결과 비교

 

답)

 

1. 두 노드를 잇는 가장 짧은 경로를 찾는 최단경로 문제 개요

가. 최단경로 문제의 분류

최단경로 문제를 해결하기 위한 알고리즘에는 4가지 유형의 알고리즘이 존재

 

나. 최단경로 알고리즘 유형 4가지 종류

다익스트라 알고리즘	한 정점에서부터 다른 모든 정점으로의 최단 경로를 구하는 알고리즘
A* 알고리즘	탐색속도를 높이기 위해 휴리스틱 방법을 사용하여 최단 경로를 구하는 알고리즘
벨만-포드 알고리즘	음수 가중치가 있고, 음수 사이클이 없는 그래프에서 한 정점으로부터 다른 모든 정점으로의 최단 경로 및 거리를 구하는 알고리즘
플로이드와샬 알고리즘	모든 정점 사이의 최단경로 및 최단 거리를 구하는 알고리즘

 

2. 다익스트라 알고리즘과 A* 알고리즘을 이용한 최단경로 계산

가. 다익스트라 알고리즘을 이용한 최단경로 계산

계산
설명	1) 모든 정점 위에 있는 경로의 길이를 무한대(∞)로 초기화 2) 시작 정점 경로 길이를 0으로 초기화하고 최단 경로에 추가 3) 최단 경로에 새로 추가된 정점의 인접 정점들에 대하 경로 길이를 갱신하고 이를 최단 경로에 추가 4) 추가하려는 인접 정점이 이미 최단 경로에 존재한다면 이전 경로 길이와 비교하여 작으면 수정, 크면 무시 5) 그래프 내의 모든 정점들이 최단 경로로 만들어질 때까지 반복
다익스트라 알고리즘을 이용하여 링크스테이트 라우팅 기법에서 최단 경로를 계산

 

나. A* 알고리즘을 이용한 최단경로 계산

계산
설명	1) 시작정점으로부터 목표정점 방향의 가장 근접한 정점 선택 (휴리스틱 함수 사용) 2) 이미 조사된 정점을 닫힌 목록으로, 조사대상의 정점을 열린 목록으로 규정 3) 열린 목록에서 가장 유망한 정점을 취하며 조사된 정점은 닫힌 목록으로 소속 4) 목표정점에 도달할 때까지 열린 목록을 조사하여 닫힌 목록으로 변환시키는 작업을 반복 수행

 

 

3. 벨만포드 알고리즘과 플로이드와샬 알고리즘을 이용한 최단경로 계산

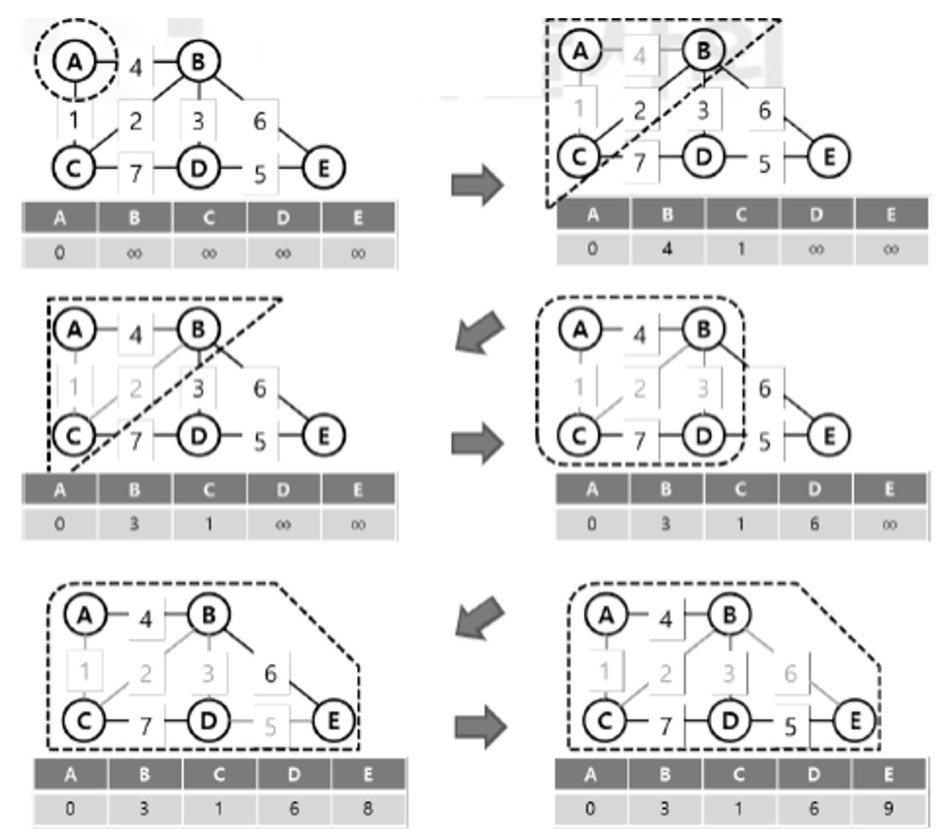
가. 벨만포드 알고리즘을 이용한 최단경로 계산

 

계산
설명	1) 모든 정점 들은 경로의 길이를 무한대(∞)로 초기화 2) 시작 정점의 길이를 0으로 초기화하고 최단 경로에 추가 3) 음의 가중치를 고려하면서 연결된 정점들의 경로의 길이를 갱신 4) 인접한 정점이 최단 경로에 이미 존재하면, 이전 경로 길이와 비교하여 작으면 수정, 크면 무시 5) 그래프 내의 모든 정점들이 최단 경로로 만들어질 때까지 반복
벨만포드 알고리즘을 이용하여 거리벡터 라우팅 기법에서 최단 경로를 계산

 

나. 플로이드와샬 알고리즘을 이용한 최단경로 계산

 

계산
설명	1) 정점과 간선 정보를 담고 있는 행렬을 생성 2) 행렬을 통해 해당 값을 구함 3) 모든 정점과 간선이 최단 경로를 구할 때까지 반복
플로이드와샬 알고리즘은 모든 정점 사이의 최단거리를 구할 수 있는 것이 특징

4. 최단경로 알고리즘 유형 간 결과 비교

 

비교항목	다익스트라	A*	벨만포드	폴로이드와샬
최단거리 계산(A~E)	9	10	9	10
탐색경로	단일 정점 출발	단일 쌍 정점 계산	단일 정점 출발	모든 정점 계산
구현방식	Greedy 기법	Greedy 기법	Greedy 기법	동적계획법
특징	최소비용 경로 설정	휴리스틱 순서 탐색	음의 가중치 계산	동적계획 기반
응용분야	링크상태 라우팅	네비게이션	거리벡터 라우팅	GIS 네트워크 분석

 

---

 

공감과 댓글은 아이티신비에게 큰 힘이 됩니다.

블로그 글이 유용하다면 블로그를 구독해주세요.♥