78. 다음 중 리눅스의 파일 종류로 가장 적절하지 않은 것은?
① FIFO 파일 ② 가상 파일
③ 일반 파일 ④ 디렉토리 파일
■ 해설
- FIFO 팔일 : 일반적으로 named pipe 라고 부르며 프로세스 통신인 IPC 를 위해 사용됨
- 일반파일 : 가장 흔한 파일 종류로 텍스트, 이미지, 로그 등 우리가 흔히 알고 있는 파일
- 디렉토리 파일 : 리눅스에서 Is 명령어를 통해 확인해 보면 다른 파일 및 다른 디렉토리를 포함할 수 있는 파일 시스템 구조를 저장하고 있는 파일
- 가상파일 : 이 항목을 선택하신 분들은 심볼릭 링크(윈도우에서 아이콘 같은 역할)가 가상의 대상을 지정하고 있다고 혼선이 생길 수 있는데 심볼릭 링크를 명확하게 가상파일이라고 부르지는 않습니다. 또한 리녹스 안에 컨테이너, Virtual Machine 을 설치할 수 있기에 이 파일들도 가상파일과 혼선될 수 있으나 리눅스 OS 자체에서 분류하고 있지 않은 외적인 파일 체계라고 보입니다.
정답 : ②
79. 다음 그림은 전가산기(full adder) 4개를 사용한 4비트 가산기를 나타낸 것이다. 2의 보수로 표현된 수들 간의 덧셈에서 상태 비트 제어 회로의 오버플로우 플래그(V) 논리식으로 가장 적절한 것은?
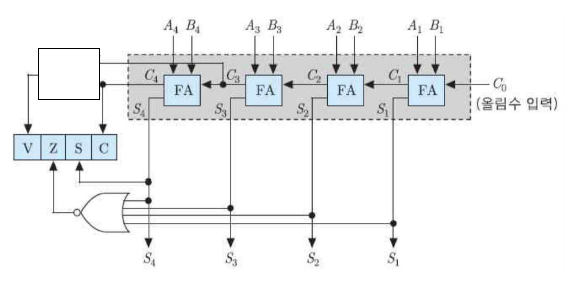

■ 해설
- 이 문제는 2진수의 숫자 표현 방식을 1차적으로 학습하고
- 2complement(2의 보수) 로 표현되는 음수 표현을 이해하고
- 가산하는 동작에서 발생되는 sum 과 carry에 대해서 생각해볼 기회를 가졌었다면
- 오버플로우의 조건이 맨 끝 두자리의 carry 결과가 다를 때 발생된다는 것을 알아야 풀 수 있는 문제입니다.
아래와 같은 4비트 체계의 2진수를 생각해 봅니다.
|
10진수 양수
|
2진수 양수(2의 보수)
|
10진수 음수
|
2진수 음수(2의 보수)
|
|
0
|
0000
|
0
|
0000
|
|
1
|
0001
|
-1
|
1111
|
|
2
|
0010
|
-2
|
1110
|
|
3
|
0011
|
-3
|
1101
|
|
4
|
0100
|
-4
|
1100
|
|
5
|
0101
|
-5
|
1011
|
|
6
|
0110
|
-6
|
1010
|
|
7
|
0111
|
-7
|
1001
|
|
|
|
-8
|
1000
|
- 2의 보수에서 음수는 양수를 1→0, 0→1 로 변환하고 1을 더하면 됩니다.
- 양수 음수 표현에서 양수는 항상 음수보다 1개 적습니다,(8bit 체계는 -128 ~ 127)
- 오버플로우란 연산의 결과가 주어진 데이터의 표현 범위를 넘어서서 양수가 음수로 음수가 양수로 변경되는 현상을 말합니다.
|
예시
|
십진수 계산
|
이진수 계산(설명을 위해 [] <> 사용
|
설명
|
|
3+4
|
3+4=7
(결과는 데이터 표현 범위 안) |
[0]<0>11 위와 아랴의 합은 0111
[0]<1>00 (2진수 양수 결과) |
C3<>의 carry 는 0
C4[] 의 carry 는 0 둘 다 자리 올림이 없어 0으로 같음(오버플로우X) |
|
4+4
|
4+4=8
(결과는 데이테 표현 범위 밖) |
[0]<1>00위와 아래의 합은 1000
[0]<1>00 (-8 음수로 부호 바뀜) |
C3<>의 carry 는 1
C4[]의 carry 는 0 C3 만 자리올림이 있어 carry 가 다름(오버플로우O) |
|
(-4)+(-4)
|
(-4)+(-4)=-8
(결과는 데이터 표현 범위 안) |
[1]<1>00 위와 아래의 합은 1000
[1]<1>00 (2진수 음수 결과) |
C3<>의 carry 는1
C4[] 의 carry는 1 둘 다 자리 올림이 있어 1로 갈음(오버플로우 X) |
|
(-4)+(-5)
|
(-4)+(-5)=-9
(결과는 데이터 표현 범위 밖) |
[1]<1>00 위와 아래의 합은 0111
[1]<0>11 (7 양수로 부호 바뀜) |
C3<> 의 carry는 0
C4[]의 carry는 1 C4 만 자리올림이 있어 carry 가 다름(오버플로우O) |
따라서, 오버플로우의 결정은 C3와 C4가 다를 경우에만 발생합니다. (C3 (+) C4)
● 병렬 가산기(parallel adder)
- 덧셈을 수행하는 하드웨어 모듈
- 비트 수만큼의 전가산기(full-adder)들로 구성
- 덧셈 연산 결과에 따라 해당 조건 플래그들(condition flags) 을 세트
- C 플래그 : 올림수(carry)
- S 플래그 : 부호(Ssign)
- Z 플래그 : 0(zero)
- V 플래그 : 오버플로우(overflow)
- 4-비트 병렬 가산기와 상태 비트 제어회로

정답 : ④
공감과 댓글은 아이티신비에게 큰 힘이 됩니다.
블로그 글이 유용하다면 블로그를 구독해주세요.♥
'정보시스템 감리 기출해설 > 시스템 구조 해설' 카테고리의 다른 글
| (제 25회) 시스템 구조 / (82)~(83) 해설 (0) | 2025.02.09 |
|---|---|
| (제 25회) 시스템 구조 / (80)~(81) 해설 (0) | 2025.02.08 |
| (제 25회) 시스템 구조 / (76)~(77) 해설 (0) | 2025.02.06 |
| (제 22회) 시스템 구조 / (98)~(100) 해설 (1) | 2024.12.16 |
| (제 22회) 시스템 구조 / (96)~(97) 해설 (0) | 2024.12.15 |