가설검증

문제3) 한 공장에서 스마트 팩토리(Smart Factory) 적용을 통한 생산시간 단축을 확인 하려고 한다. 기존 공정에서의 제품 생산시간이 정규분포를 따르며 평균이 30분, 표준 편차가 5분인 것으로 알려져 있다. 스마트 팩토리가 적용된 공정의 제품에 대한 생산 시간을 49개 랜덤 추출하여 관측한 결과 평균이 28.5분이었다. 스마트 팩토리가 적용된 공정의 생산시간이 표준편차가 5분인 정규분포를 따른다고 할 때, 스마트 팩토리를 통해 생산시간이 단축되었는지 가설을 설정하고 검정 하시오. (단, 유의수준 5%, Z0.005=1.645)

 

답)

 

 

1. 통계 추론 분야에서의 가설 검정의 개요

가. 가설 검정의 개념(Testing hypothesis)

• 통계 추론 분야에서 가설 검정은 표본에 담긴 정보를 이용하여 가설의 옳고 그름을 통계적으로 판정하는 학문 분야.
• 수집된 표본 결과가 확률적 오차를 수반하므로 오류의 허용 확률을 미리 정해 놓고 그 기준에 따라 가설의 채택이나 기각을 결정

 

나. 가설 검정에서 귀무가설과 대립가설 및 유의 수준

구분	설명
귀무가설, H0	Null hypothesus 대립가설이 참이라는 확실한 근거가 없는 경우에 받아들이는 가설 즉, 대립가설이 참이 아닌 가설
귀무가설, H1	Alternative hypothesis 표본으로부터 확실한 근거에 의하여 입증하고자 하는 가설을 대립가설이라고 함 즉, 분석지수가 주장하는 가설, 모집단의 특성에 대한 새로운 사실이나 주장하는 가설
유의 수준	귀무가설 H0 가 참일 때 대립가설 H1 을 채택하는 오류를 병할 확률의 최대 허용 한계

 

2. 가설 검정의 절차

구분	설명
가설의 설정	연구의 목적이 되는 대립가설과 이에 반대되는 귀무가설을 설정
유의수준 결정	적용하고자 하는 유의수준을 결정하다. 보통 95%의 신뢰수준을 유지하는 선에서 결정되지만, 때에 따라서 99%를 유의수중으로 결정할 수도 있다
적절한 통계방법 결정	각 변수는 척도에 따라 t분포, F분포, x² 분포 등 다양한 형태의 확률분포를 보이므로, 적용하고자 하는 변수 즉, 독립변수와 종족변수가 각각질적 수준인지 양적 수준인지를 잘 파악하고 적절한 통계분석방법의 결정이 중요하다
가설의 기각과 채택 결정	계산된 검정통계량에 대한 유의확률을 유의수준과 비교하여 귀무가설의 기각과 채택을 결정한다
결과를 해석	귀무가설의 기각과 채택여부에 따라 결과를 해석하고 결론을 맺게 된다

 

3. 사례를 통한 가설 검정의 문제 풀이

가. 가설의 수립

• 귀무 가설: 생산 평균 시간이 30분이다. 즉, 스마트팩토리를 통해 생산시간 단축 없음 (Η0: = 100
• 대립 가설: 생산 평균 시간이 30분 이상이다. 즉, 스마트팩토리를 통해 생산시간 단축 있음 (H1: > 10)

 

나. 유의 수준의 설정

• 주어진 표본 평균이 표준 정규 분포를 따른다고 가정하면 Z0.05 = 1.645이므로 아래의 그림과 같이 구간을 설정하여 채택 역과 기각 역을 설정

즉, 위의 그림과 같이 유의 수준 5%이내는 표준정규분포로 나타내었을 때에 1.645인데, 이 값보다 작으면귀무 가설을 채택하고, 클 경우에는 귀무 가설을 기각하고 대립 가설을 채택한다.

 

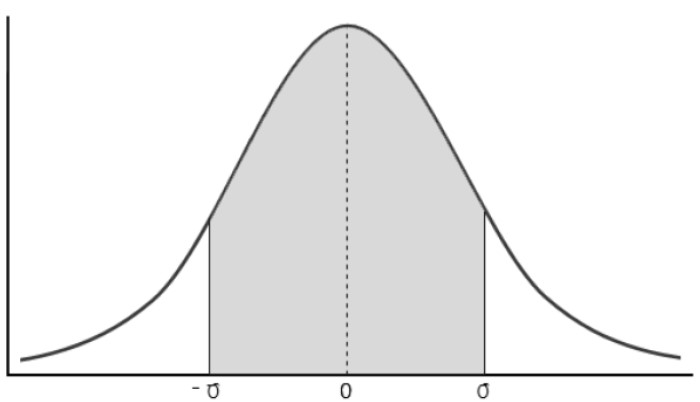4. 결과 산출 및 해석

가. Z값 산출 및 분석

• 주어진 표본 평균이 정규 분포를 따른다고 가정하면 -1.645 > -2.1 이므로, 귀무 가설 H0이 기각됨

 

나. 결과의 해석

• 표본 평균 28.5는 기각 역에 속하기 때문에 귀무 가설을 기각할 수 있다. 따라서, 유의수준 5% 하에서 스마트 팩토리(Smart Factory) 적용을 통한 생산시간 단축을 됨을 의미

 

---

 

공감과 댓글은 아이티신비에게 큰 힘이 됩니다.

블로그 글이 유용하다면 블로그를 구독해주세요.♥